Normalización: Escalas

Vamos a dedicarle una entrada exclusiva a las escalas, aunque sea repaso de 1º, ya que es muy probable que tengáis que aplicar escalas en el examen de acceso a la universidad.
En los apuntes recomendados sobre Normalización que os dejé en el ejercicio anterior, decía de manera resumida:

CONCEPTO DE ESCALA

Los diferentes tamaños de los objetos que proyectamos, desde un edificio a la piezas diminutas de un relog, por ejemplo, obliga a transformar las dimensiones reales de los objetos representados en otras proporcionales a ellas. 

La constante de proporcionalidad es lo que se denomina escala del dibujo y expresa la relación entre la medida lineal de la representación de un elemento de un objeto y la correspondiente medida lineal real de dicho elemento.

Fuente. DT.com

Si el numerador de esta fracción es mayor que el denominador, se trata de una escala de ampliación, y será escala de reducción en caso contrario. La escala 1:1 corresponde a un objeto dibujado a su tamaño real (escala natural).

ESCALAS NORMALIZADAS

Aunque, en teoría, sea posible aplicar cualquier valor de escala, en la práctica se recomienda el uso de ciertos valores normalizados con objeto de facilitar la lectura de dimensiones mediante el uso de reglas o escalímetros.

No obstante, en casos especiales (particularmente en construcción) se emplean ciertas escalas intermedias tales como:

• 1:25, 1:30, 1:40, etc…

Ejemplos prácticos

EJEMPLO 1

Se desea representar en un formato A3 la planta de un edificio de 60 x 30 metros.
La escala más conveniente para este caso sería 1:200 que proporcionaría unas dimensiones de 30 x 15 cm, muy adecuadas al tamaño del formato.

EJEMPLO 2:

Se desea representar en un formato A4 una pieza de reloj de dimensiones 2 x 1 mm.
La escala adecuada sería 10:1

EJEMPLO 3:

Sobre una carta marina a E 1:50000 se mide una distancia de 7,5 cm entre dos islotes, ¿qué distancia real hay entre ambos?
Se resuelve con una sencilla regla de tres:

si 1 cm del dibujo son 50000 cm reales
7,5 cm del dibujo serán X cm reales

X = 7,5 x 50000 / 1 … y esto da como resultado 375.000 cm, que equivalen a 3,75 km.

CONVERSIÓN DE ESCALA

La numeración de una escala se puede expresar en fracción quebrada y en fracción decimal. En algunos casos será conveniente saber convertir una expresión decimal en quebrada o viceversa. Veamos cómo se hace:

1. Fracción quebrada a fracción decimal: bastará dividir el numerador por el denominador. P.e. 4/5= 0,8
2. Fracción decimal a fracción quebrada: Escala:0,8 , 0,6/1=66/100=2/3

PASO DE UNA ESCALA A OTRA

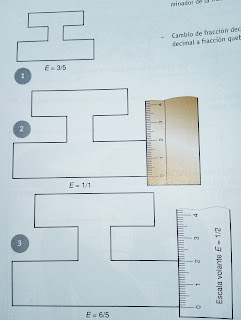En algunos casos necesitaremos pasar un dibujo que está a una escala determinada, redibujarlo a otra diferente. Por ejemplo, un dibujo que esté a a escala 3/5 pasarlo a escala 6/5.

El dibujo a escala 3/5 supone que las magnitudes reales de él son 5/3 mayores; por tanto el problema se resume en obtener las verdaderas magnitudes de dibujo y luego aplicarles el nuevo coeficiente de la nueva escala, es decir, 6/5, para así determinar el tamaño del nuevo dibujo.

Por consiguiente, la escala de relacción entre el dibujo original y el dibujo final, se obtiene al multiplicar la inversa de la escala del dibujo dado por la escala a la que se desea representar el nuevo dibujo. 

Aplicando lo expuesto a nuestro ejemplo, se tiene que: la escala original es 3/5 , su inversa 5/3 multiplicado por 6/5, es igual 30/15 = 1/2.

Otra forma de calcular la escala intermedia.
Para practicar esto realiza el ejercicio propuesto en la PAU de Andalucía junio 2014. (Página 3)

ESCALA GRÁFICA Y ESCALA VOLANTE

Basado en el Teorema de Thales se utiliza un sencillo método gráfico para aplicar una escala.
Véase, por ejemplo, el caso para ESCALA 3:5:

• Con origen en un punto O arbitrario se trazan dos rectas r y s formando un ángulo cualquiera.
• Sobre la recta r se sitúa el denominador de la escala (5 en este caso) y sobre la recta s el numerador (3 en este caso). Los extremos de dichos segmentos son A y B.
• Cualquier dimensión real situada sobre r será convertida en la del dibujo mediante una simple paralela a AB.

Fuente. DT.com

También puedes ver en el siguiente vídeo cómo dibujar una escala gráfica incluida lo se llama la contraescala, que es la subdivisión en décimas de la unidad elegida: 

ESCALA VOLANTE

La escala volante es una herramienta que nos podemos fabricar para leer las medidas sobre el dibujo con mayor agilidad. Pare ello utilizaremos uno de los lados de un folio para dibujar nuestra escala gráfica, como hemos visto en el vídeo.

10endibujo.com

EJERCICIOS. Vamos a practica todo esto en los siguientes dibujos propuestos:

TRIÁNGULO UNIVERSAL DE ESCALAS

Mediante un triángulo, podemos construir las escalas más sencillas, tanto normalizadas como no. Como vemos en las figuras, lo podremos hacer mediante un triángulo equilátero de 10 cm de lado, o mediante un triángulo rectángulo isósceles, cuyos catetos midas 10 cm.

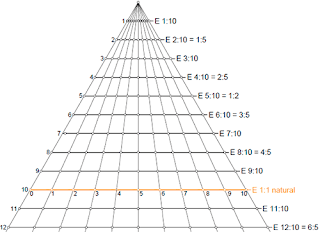
Veamos cómo se construye a través del PdD:

ESCALA DECIMAL DE TRANSVERSAL

Con este tipo de escala se puede obtener, con mayor exactitud, las medidas de un segmento a escala, ya que en la denominada contraescala, de la parte izquierda, podremos apreciar las décimas y centésimas de unidad.

En la siguiente imagen podemos ver como hemos construido la escala decimal de transversales 1:20, y en ella hemos indicado dos ejemplos de mediciones sobre la misma, 2,77 m y 1,53 m.

EL ESCALÍMETRO

En la práctica habitual del dibujo, a la hora de trabajar con escalas, se utilizan los escalímetros:

La forma más habitual del escalímetro es la de una regla de 30 cm de longitud, con sección estrellada de 6 facetas o caras. Cada una de estas facetas va graduada con escalas diferentes, que habitualmente son:

1:100, 1:200, 1:250, 1:300, 1:400, 1:500

Estas escalas son válidas igualmente para valores que resulten de multiplicarlas o dividirlas por 10, así por ejemplo, la escala 1:300 es utilizable en planos a escala 1:30 ó 1:3000, etc.

Otro modelo, menos habitual de escalímetro, es el escalímetro en abanico, compuesto por una serie de reglas en las que se han dibujado las diferentes escalas gráficas.

Os dejo dos interesantes vídeos de cómo usar el escalímetro:

Ejemplos de utilización:

Para un plano a E 1:250, se aplicará directamente la escala 1:250 del escalímetro y las indicaciones numéricas que en él se leen son los metros reales que representa el dibujo.

En el caso de un plano a E 1:5000; se aplicará la escala 1:500 y habrá que multiplicar por 10 la lectura del escalímetro. Por ejemplo, si una dimensión del plano posee 27 unidades en el escalímetro, en realidad estamos midiendo 270 m.

Por supuesto, la escala 1:100 es también la escala 1:1, que se emplea normalmente como regla graduada en cm.

APUNTES

• Me gustaron estos apuntes de la Universidad Politécnica Superior de Alicante. Muy completo con ejercicios y problemas para practicar.
• Apuntes completos sobre Normalización de la editorial Editex
• Apuntes resumidos sobre normalización, realizados por Antonio Cuesta.