Vamos a tener una visión general de este tema a través de la web DIBUFIRST donde se explica e ilustra con muchos vídeos lo que es la proporción áurea.
Euclides, en su libro "Los Elementos", define una proporción basada en la división de un segmento en su "razón extrema y media". (Fuente: Matemáticas visuales)
La definición de Euclides es:
Un segmento se dice que está dividido en su razón extrema y media cuando el total del segmento es a la parte mayor como la parte mayor a la menor. (Libro IV, Definición 3)
Actualmente a esta razón la llamamos sección áurea, la razón áurea, número de oro o la divina proporción. Usualmente se denota por la letra griega phi,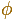 
, la inicial del nombre del escultor Phidias.
La construcción de Euclides del pentágono regular depende de esta razón. Dos diagonales de un pentágono regular que se corten dividen una a la otra en la razón extrema y media.
Usando una tira de papel podemos hacer un nudo y obtener un pentágono y un pentagrama, emblema de la escuela pitagórica. Cada segmento del pentagrama y su siguiente en tamaño están en proporción áurea. (Construye el pentagrama haciendo nudo en Matemáticas Visuales).
Geometría y Manualidades: Puedes realizar una "Estrellita inflada" aplicando este concepto.
De donde vemos que AB es igual a:
y el valor que se obtienes de este cociente lo llamamos número de oro o número áureo que se representa por la letra griega 
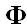(se lee FI) y vale:
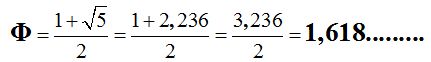
Las construcciones exactas del pentágono regular se deben a Hipócrates y se basan en la proporción áurea pues la razón entre la diagonal y el lado del pentágono es igual a Ф: d/l=Ф.
Para construir el pentágono basta con realizar una triangulación colocando adecuadamente lados y diagonales. (Ver demostración matemática en "Matemáticas Visuales")
Cuando el dato es la diagonal: Utilizamos otra construcción de la segmentación áurea.
QUE ES LA PROPORCIÓN ÁUREA
Euclides, en su libro "Los Elementos", define una proporción basada en la división de un segmento en su "razón extrema y media". (Fuente: Matemáticas visuales)
La definición de Euclides es:
Un segmento se dice que está dividido en su razón extrema y media cuando el total del segmento es a la parte mayor como la parte mayor a la menor. (Libro IV, Definición 3)
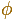, la inicial del nombre del escultor Phidias.La construcción de Euclides del pentágono regular depende de esta razón. Dos diagonales de un pentágono regular que se corten dividen una a la otra en la razón extrema y media.
Usando una tira de papel podemos hacer un nudo y obtener un pentágono y un pentagrama, emblema de la escuela pitagórica. Cada segmento del pentagrama y su siguiente en tamaño están en proporción áurea. (Construye el pentagrama haciendo nudo en Matemáticas Visuales).
Geometría y Manualidades: Puedes realizar una "Estrellita inflada" aplicando este concepto.
EL RECTÁNGULO ÁUREO
Se llama rectángulo áureo al que tiene el lado mayor en proporción áurea con el menor. Es decir:
DEMOSTRACIÓN
Para demostrarlo vamos a seguir el siguiente procedimiento:
- Construye un cuadrado de 2 cm x 2 cm. (Fuente. Aula fácil)
- Después divide el lado base en dos partes iguales de 1 cm cada una y unimos el punto medio de ese lado con el vértice superior derecho.
- Transporta el segmento r sobre la prolongación del lado de la base. Para ello traza la circunferencia de radio r y centro mitad de lado base.
Se forma un triángulo rectángulo cateto menor 1 cm, cateto mayor 2 cm e hipotenusa r. Queremos saber cuanto vale r. Si aplicamos el teorema de Pitágoras tendremos:
Si continuamos trazando el rectángulo de lados AB y 2 tenemos:
Si divides el valor del lado mayor entre el lado menor, tenemos:
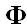(se lee FI) y vale: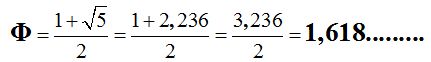Fué Leonardo Da Vinci, en el s. XVI que dio nombre a esta proporción. Pero ya los griegos, varios siglos antes de Cristo, la aplicaron en sus construcciones. También siglos atrás, en la pirámide Keops aparece.
EJERCICIOS
- Comprueba que el DNI tiene la la proporción áurea.
- Comprueba que el DNI tiene la la proporción áurea.
CONSTRUCCIONES
1. Dado un segmento determinar el segmento áureo
2. Determinar un segmento conocido el segmento áureo
Recordemos que este trazado se emplea para dibujar el pentágono regla conocido el lado porque la diagonal y el lado del pentágono están proporción áurea. (Ver demostración matemática en Matemáticas Visuales).
3. Trazados del pentágono (Fuente)
Las construcciones exactas del pentágono regular se deben a Hipócrates y se basan en la proporción áurea pues la razón entre la diagonal y el lado del pentágono es igual a Ф: d/l=Ф.
DADO EL LADO
Cuando el dato es el lado AB: dibujamos el cuadrado de lado AB y la mediatriz de dicho lado. Con centro en N y radio NM trazamos un arco que corta a la prolongación de AB en el punto P. AP es la diagonal del pentágono, pues AP/AB=Ф.Para construir el pentágono basta con realizar una triangulación colocando adecuadamente lados y diagonales. (Ver demostración matemática en "Matemáticas Visuales")
DADO EL RADIO
Cuando el dato es el radio: Dibujamos la circunferencia circunscrita, hallamos la mediatriz de un diámetro y la de uno de los radios que contiene. Con centro en P y radio PA trazamos un arco que corta al diámetro en Q. El segmento PQ es el lado del pentágono inscrito.
DADA LA DIAGONAL
Cuando el dato es la diagonal: Utilizamos otra construcción de la segmentación áurea.
Por un extremo de d trazamos un segmento perpendicular de magnitud d/2 y dibujamos el triángulo rectángulo AMP de catetos d y d/2. Con centro en P y radio PH trazamos un arco que corta a la hipotenusa en el punto Q. Con centro en A trazamos un arco de radio AQ que corta a d en el punto B.
AB es el lado del pentágono regular de diagonal d, ya que d/AB=Ф.
TRIÁNGULO DE ORO
Se llama así al triángulo isósceles de ángulos 36º y 72º, cuyos lados son la diagonal y el lado de un pentágono regular.
 |
| Fuente:Pauloporfa |
ESPIRAL LOGARÍTMICA DEL TRIÁNGULO DE ORO
Podemos trazar una espiral logarítmica a partir del triángulo de oro.
Para saber más sobre el trazado de la espiral logarítmica, visita la página "La nube artística".
4. RECTÁNGULO ÁUREO
El rectángulo áureo tiene sus lados relacionados en proporción áurea.
La construcción del rectángulo áureo está basado en la siguiente propiedad: al substraer la imagen de un cuadrado igual al de su lado menor, el rectángulo resultante es igualmente un rectángulo dorado.
ESPIRAL LOGARÍTMICA A PARTIR DEL RECTÁNGULO ÁUREO
Podemos hacer sucesivas descomposiciones del rectángulo áureo en sus correspondientes cuadrados y rectángulos áureos y trazando un arco en cada cuadrado, obtendremos la espiral logarítmica a o espiral de Durero. (Ver gráfico en Matemáticas visuales)
EJERCICIOS RECTÁNGULO ÁUREO
- Contruye la espiral de Durero.
- Sección áurea. Resumen
- Imprime y realiza los ejercicios
- Rectángulo áureo conociendo el lado menor
- Rectángulo áureo conociendo lado mayor
- Rectángulo áureo dada su diagonal
- Rectángulo áureo conociendo su perímetro
- Trazar un rombo dadas las suma de sus diagonales, sabiendo que están en proporción áurea.
- A partir de un triángulo rectángulo de 60 mm de hipotenusa y cuyos catetos estén en proporción áurea, realiza una composición en espiral utilizando seis triángulos semejantes menores y de forma que el cateto mayor sea la hipotenusa del siguiente.
- Dibujar un óvalo conociendo que los ejes están en proporción áurea.
APUNTES Y ENLACES DE INTERÉS
- Apuntes muy completos e interesantes en el blog de fotografía digital Paoloportal.
- EL RECTÁNGULO ÁUREO. Demostración matemática del trazado de un rectángulo áureo dado el lado menor.
- En el estraordinario blog "Matemáticas visuales" encontramos varias explicaciones e imágenes interactivas de gran interés:
- 1. La proporción áurea y el rectángulo áureo demostración.
- 2. El rectángulo áureo.
- 3. La diagonal en un pentágono regular y la proporción áurea.
- 4. Dibujo del pentágono regular dado el lado con compás.
- La sección áurea y la construcción de polígonos regulares. Artículo que puede servir, al menos la primera parte, como unos buenos apuntes del tema.
- El número de oro y la sección áurea en "La espiral cromática". Os incluyo la presentación con muchos ejemplos.
VÍDEOS
- Te recomiendo la película de WalT Disney "Donald en la tierra mágica de las matemáticas" para tener una visión de conjunto del tema de una manera muy amena.
- min. 7. La proporción áurea.
- min.17. El billar y los cálculos.
- Vídeo sobre las proporciones del rostro humano y la belleza.
No hay comentarios:
Publicar un comentario