Tangencias III. Inversión. Aplicación a la resolución de tangencias

De Melchoir - Trabajo propio, CC BY-SA 3.0, Enlace

5. RECTA Y CIRCUNFERENCIA INVERSA

En el primer capítulo de" Inversión I: Definición y propiedades", uno de los últimos capítulos del tema es la figura inversa de una recta.

Recordamos:

• La figura inversa de una recta (que no pase por O) es una circunferencia que pasa por el centro de inversión.
• Recíprocamente la figura inversa de una circunferencia que pasa por el centro de inversión es una recta.

Conociendo esto podemos enunciar que: 

Dadas una recta y una circunferencia pueden considerarse inversas en dos inversiones, una positiva y otra negativa, cuyos centros de inversión son los extremos del diámetro perpendicular a la recta.

6. TANGENTE EN UN PUNTO DE LA CIRCUNFERENCIA INVERSA DE UNA RECTA

Ver en Geogebra

La tangente t, en un punto B de una circunferencia con la recta s, que contiene al punto homólogo del punto de tangencia, forma un ángulo alfa igual al que forma s con la recta, r, figura inversa de la circunferencia.

Puedes hacer la demostración con geogebra como muestran ambos dibujos: inversión positiva e inversión negativa.

7. CIRCUNFERENCIA TANGENTE A OTRA Y A UNA RECTA

Si los ángulos B y B' son iguales el triángulo BRB' es isósceles, sus lados iguales están, uno sobre la tangente t a la circunferencia en B, y el otro sobre la recta r inversa de la circuferencia O1.

O2, tangente a los lados del triángulo en B y B' lo será a la circunferencia dada, O1, y a su recta inversa, r.

Los puntos de tangencia de la circunferencia tangente a otra dada y a una recta son homólogos en la inversión que liga a la circunferencia dada y a la recta. 

Por este procedimiento pueden resolverse de forma rápida, los problemas de tangencia siguientes resueltos por potencia:

• 5. Circunferencias tangentes a otra y a una recta, dado el punto de tangencia sobre la recta.
• 6. Circunferencia tangente a otra en un punto de ella y a una recta dada.

Ver en Geogebra

Ver en geogebra

Además, la circunferencia O2 es inversa de sí misma, ya que pasa por dos puntos B, B' homólogolos en la inversión, con lo que cualquier punto P, de O2 tiene su inverso P' en ella misma y alineado con el centro de inversión, O.

8. CIRCUNFERENCIA QUE ES TANGENTE A OTRA, A UNA RECTA Y PASA POR UN PUNTO

Ver en geogebra

Si P, pertenece a O2 su homólogo pertenece tambien a O2 y está alineado con con P y el centro O' de inversión. Como además, P y P' son concíclicos con otro par de puntos homólogos, A y A', por tanto, la circunferencia que contiane a A A' y P contiene a P'.

Ver en geogebra

9. CIRCUNFERENCIAS QUE PASAN POR UN PUNTO Y SON TANGENTES A OTRA DADA Y A UNA RECTA.

Ver en geogebra

Este caso, se resuelve con dos soluciones por inversión positiva y otras dos con inversión negativa. El problema tiene un total de cuatro soluciones. Veamos los pasos por inversión positiva de las dos primeras:

1. Determinar el centro de inversión positiva O' y los homólogos A A'.
2. Encontrar el homólogo de P con ayuda de la circunferencia que pasa por AA'P.
3. Trazar las circunferencias O2 y O3 que pasan por dos puntos P P', y son tangentes a r (Ver ejercicio nº 2 por potencia).

Ahora, las dos soluciones por inversión negativa:

Ver en geogebra

1. Determinar el centro de inversión negativa O y los homólogos A A'.
2. Encontrar el homólogo de P con ayuda de la circunferencia que pasa por AA'P.
3. Trazar las circunferencias O2 y O3 que pasan por dos puntos P P', y son tangentes a r (Ver ejercicio nº 2 por potencia).

9.1 SEGUNDO MÉTODO

También se puede resolver este problema tomando como centro de inversión el punto P. Transformando la circunferencia dada en inversa de sí misma y hallando la circunferencia inversa de la recta dada.
Si atendemos a la propiedad explicada más arriba donde se conservan los ángulos en la inversión, las circunferencias solución son inversas de las rectas tangentes comunes a la circunferencia dada y a la circunferencia inversa de la recta que hayamos. El problema así planteado nos ofrece cuatro soluciones mediante una sola inversión. Se siguen los siguientes pasos:

1. Hallamos la circunferencia inversa de la recta.
2. Se trazan las tangentes exteriores e interiores a las dos circunferencias determinando los puntos de tangencia.
3. Se dibujan los inversos de los puntos de tangencia hallados contenidos en la circunferencia dada que es inversa de sí misma. Estos puntos de tangencia pertenecen a las soluciones buscadas. Ver en Geogebra

9.2. EJERCICIOS

• CRP Resuelto de otro modo en Circulandia

10. CIRCUNFERENCIA TANGENTE A UNA RECTA Y A DOS CIRCUNFERENCIAS

En su caso general, este problema tiene ocho soluciones.

Aplicamos el método gráfico de sumar y restar datos para reducir elementos y poder resolver el problema por medio de un caso ya resuelto (ejercicio nº 8). Para ello, trazamos rectas paralelas a r a una distancia igual al radio de la circunferencia menor, y hacemos lo mismo con la circunferencia mayor. Para simplificar el problema operamos solo con r' y O'.

Ahora estamos en el caso anterior:

1. Determinar el centro de inversión negativa o positiva O y los homólogos A A'.
2. Encontrar el homólogo de P con ayuda de la circunferencia que pasa por AA'P.
3. Trazar las circunferencias O2 y O3 que pasan por dos puntos P P', y son tangentes a r (Ver ejercicio nº 2 por potencia).
4. Volviendo al radio origen podemos dibujar dos de las soluciones buscadas.

Estudiemos el problema a través de los trabajos realizados por otros profesores:

•  los problemas resueltos (CCR) y de la presentación elaborada por el profesor Gonzalo Avella:

Rcc from gonzalo arratibel

• Por Luis Pérez, veamos aquí uno de los casos.
• Por dibujo técnico.com
• Un caso particular por Jose Ángel Suarez

11. CIRCUNFERENCIAS INVERSAS

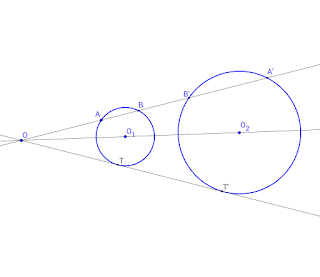Ver Geogebra

Dadas dos circunferencias, si se determina su centro de homotecia correspondiente (de razón positiva o negativa), y se permutan los puntos homólogos, tenemos que:
OA/OB' = OB/OA'

OA . OA' = OB . OB' = K

Los que demuestra que dos circunferencias (no tangentes, ni concéntricas) son inversas con centros de inversión coincidentes con los de la homotecia.

Multiplicando los miembros de la igualdad, resulta:

OA . OA' . OB . OB' = K2 (cuadrado)

Pero,
OA . OB  = OT2  y  OA' . OB' = OT'2
Sustituyendo,
OT2  . OT'2 = K2,

OT . OT' = K

Es decir, que los puntos de tangencia de las tangentes comunes (exteriores o interiores) son homólogolos en la inversión (positiva o negativa) que liga a las circunferencias.

Ver en Geogebra

12. TANGENTES EN PUNTOS HOMÓLOGOS DE DOS CIRCUNFERENCIAS.

Ver en Geogebra

En la inversión de dos circunferencias las rectas tangentes en puntos homólogos, forman el mismo ángulo con las rectas que unen dichos puntos con el centro de inversión.

De lo que se deduce que:

• En la inversión se conservan los ángulos.

• Las tangentes a dos circunferencias en puntos homólogos, en la inversión, se cortan en el eje radical de las circunferencias.

Pasará lo mismo en la inversión negativa. Os dejo a vosotros que lo comprobéis con el dibujo pertinente.

13. CIRCUNFERENCIAS TANGENTES A OTRAS DOS INVERSAS

Ver en geogebra

Puesto que los triángulos BRB' y AR1A' son isósceles, prolongando los radios de las circunferencias O1 y O2 que pasan por los puntos homólogos B B' (AA'), se determinan los centros O3 y O4 de circunferencias tangentes a las inversas O1 y O2.

Pasaría lo mismo en la inversión negativa. Os animo a que hagáis vosotros el dibujo.

Por tanto,
Por puntos homólogos en la inversión de dos circunferencias pasan circunferencias tangentes a ellas. Además estas circunferencias son inversas de sí mismas.

14. INTERSECCIONES DE LAS CIRCUNFERENCIAS TANGENTES A OTRAS DOS INVERSAS

Ver en geogebra

Siendo O3 y O4 inversas de sí mismas. Si tomamos el punto P de la intersección entre ellas, debe cumplirse, tanto en uno como en otra:

OA . OA' = OB . OB' = PO . OP' = K

Lo que demuestra que el otro punto de intersección, P', está alineado con P y O, en definitiva es el inverso de P y convierte a la circunferencia O1 en la O2. 

Por tanto:

Los puntos de intersección entre dos circunferencias, tangentes a otras dos dadas, son homólogos en las inversiones que ligan a las dos circunferencias dadas.

Esto sucede en la inversión positiva, como vemos en la imagen, como en la negativa, que espero hagáis el dibujo para comprobarlo.

15. DADAS DOS CIRCUNFERENCIAS Y UN PUNTO, TRAZAR LAS CIRCUNFERENCIAS TANGENTES A LAS DADAS QUE PASAN POR EL PUNTO.

Ver en Geogebra

Dos soluciones por inversión positiva:

1. El centro de inversión positiva se encontrará al trazar las tangentes exteriores a las circunferencias dadas en T1 y T2.
2. Hallamos el homólogo de P por medio de una circunferencia auxiliar que pasa por P, T1 y T2, por ser puntos concíclicos y T1 y T2 homólogos. Las circunferencias buscadas pasarán por P y P'.
3. Determinar las circunferencias que pasan por dos puntos P y P' y son tangentes a una de ellas, por ejemplo a O2 (Problema nº 4 de tangencias resueltas por potencia).

Para resolver esta última parte se ha utilizado como circunferencia auxiliar la P T1 T2 P', ya secante a las dadas. Hemos hallado los puntos de tangencia T1'' y T2'' sobre la circunferencia mayor, con la intención de disminuir los errores propios del dibujo, que serían mayores utilizando la circunferencia pequeña.

Los puntos de tangencia T1' y T2' sobre la circunferencia O1, son inmediatos, pues son inversos de T1'' y T2''.

Dos soluciones por inversión negativa:

Os animo a realizar el problema con Geogebra.

15.1 SEGUNDO PROCEDIMIENTO

También se puede resolver el problema tomando como centro de inversión el punto P y transformando la circunferencia O2 en inversa de sí misma y la otra en inversa de de O1' con la misma potencia de inversión, PT.

Recordando que los ángulos se conservan en la inversión, las circunferencias solución son las inversas de las rectas tangentes comunes a O1' y O2. Con este procedimiento obtenemos las cuatro soluciones mediante una sola inversión.

Ver en Geogebra

Observa cómo se han obtenido O1' determinando primero T1':

PT1.PT′1=PT2

PT′1=PA 

Siendo A' el homólogo de A
Vemos que:

PA⋅PA′=PT2

Con lo cual,

       PA′=PT′1

Se han trazado solo una recta tangente exterior y otra interior a O1 y O1' para no complicar la construcción. Los puntos de tangencias T1''' y T3''' se obtienen de los inversos correspondientes alineados con P,  T1'' y T3'' y sobre la circunferencia inversa de sí misma.

15.2 EJERCICIOS

• CCP en circunlandia. Resuelto por inversión negativa.
• Dadas dos circunferencias y un punto de tangencia sobre una ellas trazar las circunferencias tangentes.

16. CIRCUNFERENCIAS TANGENTES A OTRAS TRES DADAS.

De Melchoir - Trabajo propio, CC BY-SA 3.0, Enlace

Este caso también se conoce como el problema de Apolonio. 

Aplicando las dilataciones, a fin de reducir una de ellas a un punto, se resulve el problema reduciéndolo al caso anterior. En el caso general se obtienen ocho soluciones:

• Centro de homotecia directo Hd, y diferencia de radios (R”’-R’ y R”-R’). Dos soluciones. FIG. 39.
• Centro de homotecia directo Hd, y suma de radios (R”’+R’ y R”+R’). Dos soluciones.
• Centro de homotecia inverso Hi, sumando a O”’ y restando a O” el radio R’. (R”’+R’ y R”-R’). Dos soluciones.
• Centro de homotecia inverso Hi, restando a O”’ y sumando a O” el radio R’. (R”’-R’ y R”+R’). Dos soluciones.

De WillowW - Trabajo propio, CC BY-SA 3.0,
https://commons.wikimedia.org/w/index.php?curid=4557488

La tangencia entre circunferencias se conserva si sus radios varían en cantidades iguales. 

Una circunferencia solución (en rosa) se debe reducir o ampliar junto con las circunferencias que sean tangentes interiormente (la circunferencia negra de la derecha), mientras que las circunferencias tangentes exteriormente (las dos circunferencias negras de la izquierda) hacen la transformación contraria.

De WillowW - Trabajo propio, CC BY-SA 3.0,
 https://commons.wikimedia.org/w/index.php?curid=4548117

Una pareja de soluciones conjugadas del problema de Apolonio (circunferencias en rosa), donde las circunferencias negras son las dadas.

De WillowW - Trabajo propio, CC BY-SA 3.0,
https://commons.wikimedia.org/w/index.php?curid=4548080

Las dos rectas tangentes de los dos puntos de tangencia de una circunferencia dada intersecan al eje radical R (recta roja) de las dos circunferencias soluciones (en rosa). Los tres puntos de intersección sobre I son los polos de las rectas que unen los puntos de tangencia azules en cada circunferencia dada (en negro).

Veamos el vídeo que nos prepara el profesor Juan Carlos García:

16.1 EJERCICIOS

• CCC parte 1/4
• CCC parte 2/4 en Circulandia
• CCC parte 3/4
• CCC parte 4/4
• CCC tangentes entre sí.
• CCC intersecan en un punto.
• CCC intersecan las tres
• CCC Con dos de ellas tangentes por inversión.

 Hay otros vídeos y otras explicaciones que te pueden servir de ayuda:

16. 2 VÍDEOS:

• Educale.com
• Math Educando

16.3 ARTÍCULOS:

• Los problemas de Apolonio en la revista Suma.
• El beso de Frederick Soddy 
• Los 10 problemas de Apolonio en Piziadas

17. EJERCICIOS

• Los problemas de Apolonio en la web uno618
• Los problemas de Apolonio en la web de Gonzalo Abella.
• Tangencias guitarra
• Problema de tangencias. Cuadrado tangente a 4 circunferencias.
• Ejercicio de enlace en Circulandia.
• Figura mediante enlaces. Circunlandia
• Enlazar Puntos
• Enlace con elipse

Tangencias IV. Problemas de Apolonio

Para entender los  10 problemas de Apolonio os presente el blog de Joaquín Turina de Santos "Apolonio", donde, no solo vamos a comprender visualmente los diez problemas, además podremos disfrutar de expresiones artísticas fascinantes que ilustran la complejidad y la belleza de estos problemas.

A continuación, la presentación del profesor Juan Díaz Almagro con los 7 primeros problemas resueltos paso a paso y aplicaciones en el dibujo de piezas.

TANGENCIAS APLICANDO POTENCIA E INVERSIÓN. DIBUJO TÉCNICO 2º BACHILLERATO from JUAN DIAZ ALMAGRO

ENLACES DE INTERÉS

EJERCICIOS

• Todos los casos de Apolonio por Gonzalo Abella
• Todos los casos de Apolonio resueltos
• El problema CCC

ENLACES

• Problema de enlaces para imprimir

GEOGEBRA

• Los diez casos de Apolonio. Del blog dedicado en exclusiva Apollonius donde la geometría se convierte en arte. De Joaquín Turina

TANGENCIAS II. Resolución por ejes radicales y centros radicales

1. Circunferencia tangente a otras dos dado el punto de tangencia sobre una de ellas. (Geogebra)

Circunferencias tangentes a otras dos, dado el punto de tangencia en una de ellas.Por potencia from Plástica Alagón


Las circunferencias solución deberán tener la misma potencia que las dadas respecto de un centro radical, que debe permanecer, forzosamente, al eje radical de las dadas. Puesto que las soluciones deben ser tangentes a la circunferencia con el punto de tangencia dado, el eje radical correspondiente a dichas soluciones será además tangente en ese punto de tangencia.
En la intersección de ambos lugares se encontrará el centro radical, a partir del cual será sencillo determinar los puntos de tangencia.

2. Trazar las circunferencias tangentes a una recta, que pasen por dos puntos. Geogebra

Los centros solución han de estar sobre la mediatriz de los puntos dados.

Hallaremos un punto P en r, que pertenece al eje radical de las soluciones.  P tiene la misma potencia respecto de una circunferencia cualquiera auxiliar que pasa por AB, que respecto de las soluciones.

3. Circunferencias tangentes a dos rectas y que pasen por un punto (Geogebra)

EXPLICACIÓN

Los centros estarán situados sobre la bisectriz.

Determinamos un punto P´simétrico de P respecto a la bisectriz. De esta forma se resuelve el problema reduciéndolo al caso anterior.

Este problema también se puede resolver por homotecia o inversión (Mongge):

Ver en geogebra

4. Circunferencias tangentes a un circunferencia dada y que pasan por dos puntos:

En este caso, los puntos podrán ser interiores o exteriores a la circunferencia dada. Veamos el caso cuando los puntos son exteriores:

Ver en Geogebra

A continuación, el caso cuando los puntos son interiores.

Ver en Geogebra

EXPLICACIÓN

Por AB, pasa el eje radical de las circunferencias solución. Y en la mediatriz estarán sus centros. Bastará dibujar una circunferencia auxiliar secante con la dada para determinar el eje radical que comparte la dada con las soluciones. Donde se corten ambos ejes, se determinará un punto que tenga la misma potencia respecto de la dada y las soluciones.

5. Circunferencias tangentes a otra y a una recta, dado el punto de tangencia sobre la recta.

En Mongge
En geogebra

EXPLICACIÓN

Utilizando una circunferencia auxiliar tangente a r en T, y secante a la circunferencia dada, se determina un punto en r que tiene la misma potencia  respecto de la circunferencia dada que las soluciones.

Los centros buscados están en la perpendicular a r que pasa por T.

6. Circunferencia tangente a otra en un punto de ella y a una recta dada.

En Mongge

EXPLICACIÓN

La recta tangente a la circunferencia por el punto dado es el eje radical que pertenece a las soluciones buscadas y a la dada. Donde corte este eje a r será el centro radical de las tres circunferencias. Por tanto tiene la misma potencia de P a T que las los puntos de tangencia de las soluciones en r.

7. Circunferencias tangentes a otra y a dos rectas

Geogebra circunferencias solución exteriores.
Geogebra. Circunferencias solución interiores.

EXPLICACIÓN

Este problema se resuelve por dilataciones, reduciendo el problema al caso anterior nº 2. Las dilataciones deben emplearse adecuadamente para conseguir todos los resultados posibles. Hay que ampliar y reducir para obtener las circunferencias solución tangentes interiores y exteriores a la dada.

8. Circunferencias con centros sobre una recta r que pasan por un punto de ella y son tangentes a otra circunferencia dada.

Las tangentes común a las soluciones es una recta que pasa por P y es perpendicular a r (eje radical). Para determinar el centro radical se dibuja una circunferencia auxiliar con centro en r que pase por P y secante a la dada. (Geogebra)

9. Circunferencias con centro sobre una recta que pasan por un punto dado y son tangentes a otra circunferencia dada.

Por el simétrico de P respecto a r pasarán las circunferencias solución. Por lo que, de esta manera, se reduce el problema al caso nº 4: circunferencias que pasan por dos puntos y son tangentes a otra dada. (Geogebra)

10. Circunferencias con centros en una recta, tangentes a otras dos dadas.

Se resolverá aplicando lo dicho en el párrafo anterior y utilizando las dilataciones convenientes para reducir una de las dos circunferencias a un punto. Se deben tener en cuenta las soluciones tangentes interiores y exteriores.

EJERCICIOS

• Imprime la colección de ejercicios de tangencia por potencia del IES Aldonza Lorenzo. Soluciones.
• Ejercicios de piezas y tangencias Aldonza Lorenzo. Selectividad.
• Ejercicios resueltos de selectividad paso a paso.
• Biela. Aplicación de tangencias en Trazoide con problema de potencia.
• Varios dibujo de objetos trazados con tangencias.
• Llave fija. Ejercicio de tangencias sencillo para familiarizarte con enlaces.

APUNTES

• No te pierdas la explicación de Antonio Castilla sobre como dibujar circunferencias tangentes por potencia. Descarga el esquema facilitador.

2º Bachillerato, 2ª evaluación curso 2016/17

EXAMEN: EJERCICIOS CORREGIDOS

1. Inversión. Problema 03 web uno618.
2. Tangencia por potencia. Ejercicio número 9 en este blog.
3. Ejercicio Tangencia. Pág. 32 Tomo I
4. Elipse. Problema 4 de la web de uno618.

TEMA 21:CÓNICAS: Elipse, Hipérbola y Parábola

TEMA 20:TANGENCIAS III. Apolonio

TEMA 19: Inversión III. Aplicación a la resolución de tangencias

TEMA 18: Inversión II. Dibujo de figuras inversas

TEMA 17: Inversión I. Definición y propiedades

TEMA 16: TANGENCIAS II. Resolución por ejes radicales y centros radicales
Revisa la siguiente entrada para recordar los contenidos y actividades expuestos en clase.

TEMA 15: Proporcionalidad inversa. Potencia, eje radical y centro radical
Revisa la siguiente entrada para recordar los contenidos y actividades expuestos en clase.

TEMA 14: Repaso de 1º: Tangencias I. Conceptos básicos

El 21 y 22 de diciembre, dedicamos las clases a refrescar todo lo que habéis aprendido de tangencia en el curso pasado. Necesitamos dominar estos contenidos para poder afrontar con holgura y confianza la parte de potencia e inversión aplicada a tangencias que veremos a la vuelta de vacaciones. 
Muchos de vosotros habéis decidido tomaros las vacaciones dos días antes, lo que significa que tendréis que hacer el repaso vosotros solos durante las vacaciones. A la vuelta espero que dominéis el tema para poder comenzar por potencia.
Al final del tema, os he dejado un ejercicio de PAU 2016 Madrid. Ejercicio B que quiero que tragáis resuelto y otros tantos que os iré colgando durante las fiestas.

También os recuerdo que a mediados de enero realizaremos un examen de cortes, secciones y acotación que espero que aprovechéis estas vacaciones para estudiar y realizar todas las tareas fotocopiadas que os dejé, ademas de los ejercicios que publico en el blog. 

¡Mucho ánimo!.¡Os deseo unas Felices Fiestas y también que os traiga Papa Noel muchas ganas de estudiar dibujo!. 

Tangencias I:

TANGENCIAS, ENLACES Y RECTIFICACIONES. Dibujo Técnico I de JUAN DIAZ ALMAGRO

PRELIMINARES:

Una recta y una circunferencia son tangentes cuando el radio que pasa por el punto de tangencia es perpendicular a la recta tangente.








 El lugar geométrico de los centros de las circunferencias tangentes a una recta, en uno de sus puntos, es la perpendicular a la recta en dicho punto:

CIRCUNFERENCIAS TANGENTES EXTERIORES

Considerando que en le punto de tangencia es posible trazar una recta tangente a las dos circunferencias en cuestión, se observa que por ser esta recta perpendicular a cada uno de los radios se cumple que:

Los radios que pasan por el punto de tangencia de dos circunferencias tangentes exteriores están en prolongación.

                                                                      CIRCUNFERENCIAS TANGENTES INTERIORES

Así mismo, considerando que el el punto se puede trazar una recta tangente a ambas, se obtiene en consecuencia, que debiendo ser esta recta perpendicular a cada uno de los radios, resulta que:

Los radios que pasan por el punto de tangencia de dos circunferencias tangentes interiores están superpuestos.

CONDICIONES GENERALES DE TANGENCIAS ENTRE DOS CIRCUNFERENCIAS

De lo dicho en los párrafos anteriores se deduce:

La recta que une los centros de las circunferencias tangentes (interiores o exteriores), pasa por el punto de tangencia.

Recíprocamente,
Las circunferencias tangentes a otra dad en un punto, T, de la misma tienen su centro sobre la recta que pasa por el centro sobre la recta que pasa por el centro de la dada y por el punto de tangencia, esta recta, es pues,

lugar geométrico de los centros de todas las posibles circunferencias tangentes a la dada en aquel punto de tangencia.

                                                                              CIRCUNFERENCIAS DE RADIO DADO TANGENTES A UNA RECTA

El lugar geométrico de los centros de las circunferencias de radio dado tangentes a una recta son las parelas trazadas a la recta a una distancia igual al radio dado.

CIRCUNFERENCIAS DE RADIO DADO TANGENTES EXTERIORES A UNA CIRCUNFERENCIA

El lugar geométrico de los centros de las circunferencias de radio dado tangentes exteriores a otra circunferencia dada, es otra circunferencia concéntrica de aquella, cuyo radio es igual a la suma de los radios.

DADOS TRES RADIOS, TRAZAR TRES CIRCUNFERENCIAS TANGENTES ENTRE SÍ EXTERIORES

CIRCUNFERENCIA DE RADIO DADO TANGENTES INTERIORES A OTRA CIRCUNFERENCIA DADA

CIRCUNFERENCIAS DE RADIO DADO TANGENTES A DOS RECTAS QUE SE CORTAN

CIRCUNFERENCIA DE RADIO DADO TANGENTE A UNA RECTA Y QUE PASE POR UN PUNTO P

CIRCUNFERENCIA DE RADIO DADO TANGENTE A OTRA DADA Y QUE PASA POR UN PUNTO P

CIRCUNFERENCIA QUE PASA POR UN PUNTO DADO Y ES TANGENTE A UNA RECTA, CONOCIDO EL PUNTO DE TANGENCIA

CIRCUNFERENCIA TANGENTE A OTRA DADA QUE PASA POR UN PUNTO EXTERIOR DADO, CONOCIDO EL PUNTO DE TANGENCIA

CIRCUNFERENCIAS INSCRITA Y EXINCRITA A UN TRIÁNGULO

RECTAS TANGENTES A UNA CIRCUNFERENCIA DESDE UN PUNTO EXTERIOR

Primer procedimiento:

Para cumplir la condición de tangencia es necesario que los ángulos T sean rectos.

Para determinar T constrúyase el arco capaz del ángulo recto que pasa por A, O.

Segundo procedimiento por medio de ARCO CAPÁZ

?
OTRA CONSTRUCCIÓN POR 

RECTAS TANGENTES EXTERIORES COMUNES A DOS CIRCUNFERENCIAS

Primer procedimiento por dilatación-contracción:

Este procedimiento consiste en reducir las condiciones dadas a otras que lleven a un problema ya resuelto, se dibuja una figura de análisis proporcional a la dada y se buscan y encuentran las propiedades que se exigen en su trazado. 

El procedimiento más aplicado en estos métodos es el de dilatación-contracción, que consiste en plantear el ejercicio de forma que se pueda encontrar una solución análoga; un ejemplo es cuando se reducen los datos planteados sumándolos o restándolos.

Ver procedimiento en la web uno681

Considerando la tangente T1T1´ se observa que forma parte de un trapecio rectángulo CT1T1´C´; que quedará resuelto al serlo el triángulo rectángulo C (punto T1 sin dilatar) y C´. Del que se conoce la hipotenusa y el cateto r-r´.

La base mayor del trapecio determinará el punto de tangencia T1 y su paralela por C´, T1´(análogo razonamiento para la simétrica) 

Segundo procedimiento por homotecia positiva de dos circunferencias

Se funda este procedimiento en que el punto C de intersección de las dos tangentes es el centro de homotecia positiva de las dos circunferencias, verificándose que T1 es homotético de T2, y A homotético de B. Basta pues, dadas las circunferencias de centros O y O1, trazar una recta cualquiera O1-A y por O, la paralela O-B a ella. Se unen A y B y se obtiene el punto C en la línea de centros. Para tener los puntos de tangencia se trazan arcos de centros en C y que pasen por O y O1.

RECTAS TANGENTES INTERIORES COMUNES A DOS CIRCUNFERENCIAS

Primer procedimiento dilatación

CIRCUNFERENCIAS DE RADIO DADO A DOS CIRCUNFERENCIAS

Este ejercicio tiene 8 soluciones posibles para un mismo caso:

TANGENTES EXTERIORES A AMBAS

TANGENTES INTERIORES A AMBAS

TANGENTES EXTERIORES A UNA DADA E INTERIORES A LA OTRA

CIRCUNFERENCIAS DE RADIO DADO TANGENTES A UNA RECTA Y A OTRA CIRCUNFERENCIA

Este problema tiene 4 soluciones:

?

EJERCICIOS:

• Fotocopia y realiza las láminas de Tangencias básicas de laslaminas.com
• Imprime 8 láminas de piezas donde aplicar problemas de tangencias básicos.
• PAU 2016 Madrid. Ejercicio B1. Solución

APUNTES:

• Tangencias en laslaminas.es. Colección de apuntes y ejercicios para 1º Bachillerato
• Tangencias básicas. IES Nou Derramador
• Tangencias. Web de Jose Antonio Cuadrado.